最近一直在看GAN,我一直认为只有把博客看了一遍,然后再敲一遍。这样才会有深刻的感悟。
GAN(生成式对抗网络)(, Generative Adversarial Networks )是一种深度学习模型,分布在无监督学习上。
分成两个模块:生成模型(Generative Model)和判别模型(Discriminative Model)。简单来说就是:两个人比赛,看是 A 的矛厉害,还是 B 的盾厉害。。
比如:我们有一些真实数据,同时也有随机生成的假数据。A把假数据拼命地模仿成真数据,B拼命地想把真实数据和假数据分开。
这里,A就是一个生成模型,类似于造假钞,一个劲的学习如何骗过B。B是一个判别模型,类似与警察,一个劲地学习如何分辨出A的造假技巧
然后,B的鉴别技巧越来越厉害,A的造假技术越来越逼真,成为一个一流的假币制造者。而GAN就是获得上述的两个模型。
我们需要同时训练两个模型。G:生成器。D:判别器。生成器G的训练过程是最大化判别器犯错误的概率,即判别器误以为数据是真实样本而不是生成器生成的假样本。因此,这一框架就对应于两个参与者的极小极大博弈。在所有可能的函数G和D中,我们可以求出唯一的均衡解,即G可以生成与训练样本相同的分布,而D判断的概率为1/2,意思就是D已经无法判别数据的真假。
为了学习到生成器在数据x上的分布P_g,我们先定义一个输入的噪声变量z,然后根据G将其映射到数据空间中,其中G为多层感知机所表征的可微函数。
同样要定义第二个多层感知机D,它的输出是单个标量。D(x)表示x是真实数据。我们训练D以最大化正确分配真实样本和生成样本的概率,引起我们就可以最小化log(1-D(G(z)))而同时训练G。也就是说判别器D和生成器对价值函数V(G, D)进行极小极大化博弈。
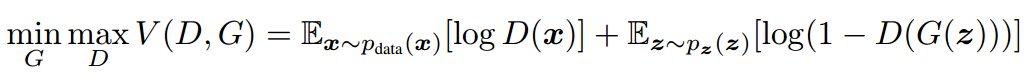

如上图所示,生成对抗网络会训练并更新判别分布(即D,蓝色的虚线),更新判别器后就能将数据真实分布(黑点组成的线)从生成分布P_g(G)(绿色实线)中判别出来。下方的水平线代表采样域Z,其中等距表示Z中的样本为均匀分布,上方的水平线代表真实数据X中的一部分。向上的箭头表示映射x = G(z)如何对噪声样本(均匀采样)施加一个不均匀的分布P_g.
(a) 考虑在收敛点附近的对抗训练:P_g和P_data已经十分相似,D是一个局部准确的分类器。
(b) 在算法内部循环中训练D,从数据中判别出真实样本,该循环最终会收敛到D(x) = P_data(x) / (P_data(x) + P_g(x))
(c) 随后固定判别器并训练生成器,在更新G后,D的梯度会引导G(z)流向更可能被D分类为真实数据的方向。
(d) 经过若干次训练后,如果G和D有足够的复杂度,那么他们就会到达一个均衡点,这时:P_g = P_data,即生成数据的概率密度函数等于真实数据的概率密度函数,生成数据 = 真实数据。在均衡点上D和G都不能进一步提升,并且判别器无法判断数据到底是来自真实样本还是伪造的数据,即D(x) = 1/2
公式推导(公式推导部分来自机器之心):
下面,我们必须证明该最优化问题也就是价值函数V(G, D),有唯一解并且该解满足P_G = P_data
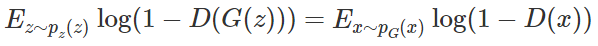
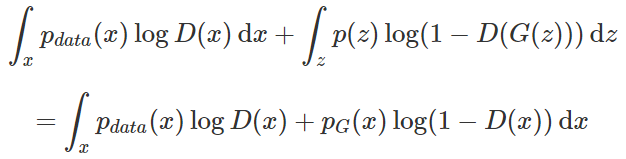
将数学期望展开为积分形式:
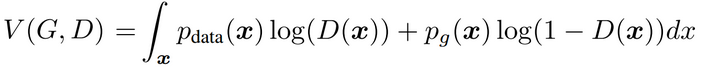
其实求积分的最大值可以转化为求被积函数的最大值。而求被积函数的最大值是为了求得最优判别器D,因此不涉及判别器的项都可以被看做为常数项。如下所示:P_data(x)和P_G(x)都为标量,因此被积函数可表示为 a * D(x) + b * log(1 - D(x)).
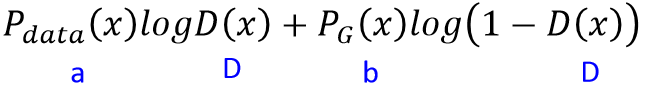
若令判别器D(x)等于y,那么被积函数可以写为:

为了找到最优的极值点,如果a + b ≠ 0,我们可以用以下一阶导求解:
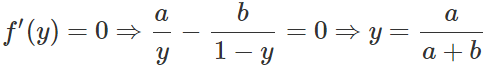
如果我们继续求表达式f(y)在驻点的二阶导:
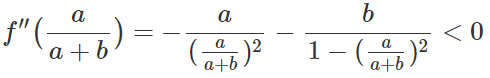

最优生成器
当然GAN过程的目标是令P_G = P_data。
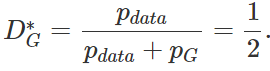
这意味着判别器已经完全困惑,它完全分辨不出P_date和P_G的区别,即判断样本来自P_data和P_G的概率都为1/2。基于这一观点,GAN的作者证明了G就是极小极大博弈的解。